
Wind AlgorithmThe ASCAT wind retrieval processing system used by NOAA was developed by the KNMI scatterometer team and adapted to the NOAA environment. The sigma-0 measurements are related to the ocean wind vectors and the radar measurement parameters via a geophysical model function (GMF). The GMF utilized in the ASCAT wind retrieval is CMOD5, and the wind retrieval is performed using the maximum likelihood estimation (MLE) principle. The harmonic characteristic of the GMF results in solutions is not unique which generally results in several ambiguities being found. The NOAA products currently include four ambiguity solutions. The NOAA Ice and Ultra High Resolution (UHR) processing algorithms were developed by Professor David Long, Brigham Young University. Geophysical Model FunctionFor the ASCAT wind products the CMOD5.n geophysical model function (GMF) for calculating equivalent neutral winds is used. This model function enables the calculation of wind speeds meeting the product requirements between 0 and 25 m/s. CMOD5.n is based on CMOD5. It is known from extensive validation work on ERS that a CMOD5 bias of 0.5 m/s against buoys persists for all wind speeds and this is compensated. Moreover, another 0.2 m/s is added to convert from real winds to equivalent neutral winds. The CMOD5.n inverted winds are thus 0.7 m/s higher than CMOD5 winds. At low wind speeds the wind direction and speed may vary considerably within the WVC. Locally, below a speed of roughly 2 ms−1 calm areas are present where little or no backscatter occurs, perhaps further extended in the presence of natural slicks that increase the water surface tension. However, given the variability of the wind within a footprint area of 25 km it is, even in the case of zero mean vector wind, very unlikely that there are no patches with roughness in the footprint. As the mean vector wind increases, the probability of a calm patch will quickly decrease, and the mean microwave backscatter will increase. Also, natural slicks quickly disappear as the wind speed increases, and as such the occurrence of these is correlated to the amplitude of the mean vector wind over the footprint, as modelled by the GMF. Low scatterometer wind speeds are thus providing useful information.
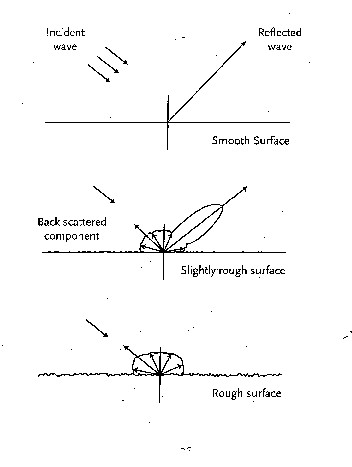
Overview of Wind Retrieval Algorithm At high wind speeds wave breaking will further intensify, causing air bubbles, foam and spray at the ocean surface, and a more complicated ocean topography. Although theoretically not obvious, it is empirically found that sigma-0 keeps increasing for increasing wind speeds from 25 m/s to 40 m/s, and that a useful wind direction dependency remains, albeit gradually weakening. Wind retrievalThe GMF has two unknowns, namely wind speed and wind direction, so, if more than two backscatter measurements are available then these two unknowns may be estimated using a maximum-likelihood estimator (MLE) as the objective function for determining wind vector solutions. The MLE is defined by the following equation
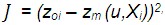 where z = (σ 0)0.625 are the transformed backscatter data, zoi are the backscatter measurements, zm (u,Xi) are the model backscatter values corresponding to the measurements. The local minima of J correspond to wind vector solutions. The three independent measurements (fore, mid and aft beam) sample the azimuth variation of the GMF in order to resolve the wind direction, albeit ambiguously. Ambiguity RemovalASCAT scatterometer winds have a multiple ambiguity and there are up to four wind solutions in each WVC on the earth's surface. These ambiguities are removed by applying constraints on the spatial characteristics of the output wind field, such as on rotation and divergence. Several ambiguity removal (AR) schemes were evaluated for ERS data in the OSI SAF Development Phase. In addition to the subjective comparison of AR schemes, a method for the objective comparison of AR performance among the different schemes was used. It has been shown that this way of comparison is effective to evaluate the shortcomings of AR schemes, but also reveals a more general way forward to improve AR, which is followed up by tuning 2D-VAR. For ASCAT this tuned version of 2D-VAR is used. |
|